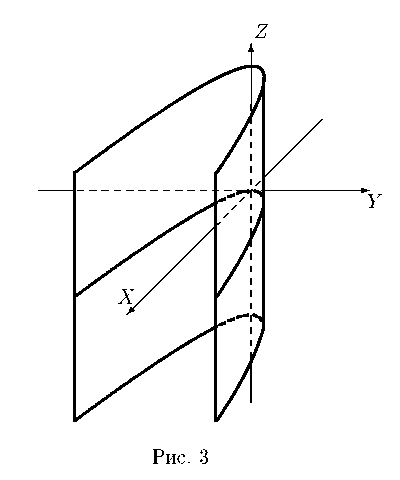Цилиндрической поверхностью называется поверхность, которая в некоторой декартовой системе координат определяется уравнением, в котором не фигурирует одна из переменных:
| F(x, y) = 0, F(x, z) = 0 или F(y, z) = 0. |
Свойство цилиндрических поверхностей.
Если некоторая точка M0(x0, y0, z0) принадлежит цилиндрической поверхности, описываемой уравнением F(x, y) = 0 , то все точкипрямой, проходящей через эту точку параллельно оси OZ , также принадлежат цилиндрической поверхности. Такие прямые называются образующими цилиндрической поверхности, а кривая, описываемая уравнением F(x, y) = 0 и получающаяся в сечении любой плоскостью z = h , называется направляющей.
Примеры цилиндрических поверхностей 2–го порядка.
Эллиптический цилиндр.Уравнение
+
= 1 (a, b>0) |
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является эллипсс полуосями a и b (рис. 1).
В частности, уравнение x2 + y2 = R2 в трехмерном пространстве определяет круглый цилиндр.
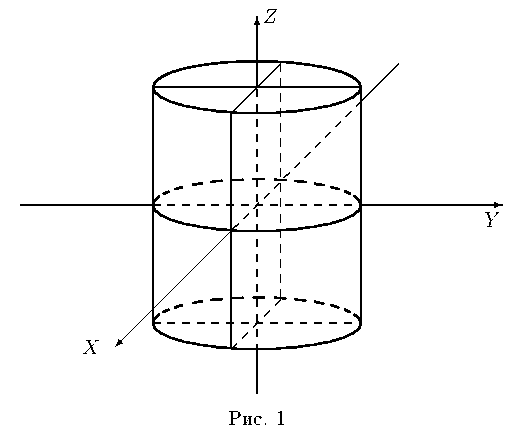
Гиперболический цилиндр. Уравнение
−
= 1 ( a, b>0 ) |
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является гиперболас полуосями a и b (рис. 2).
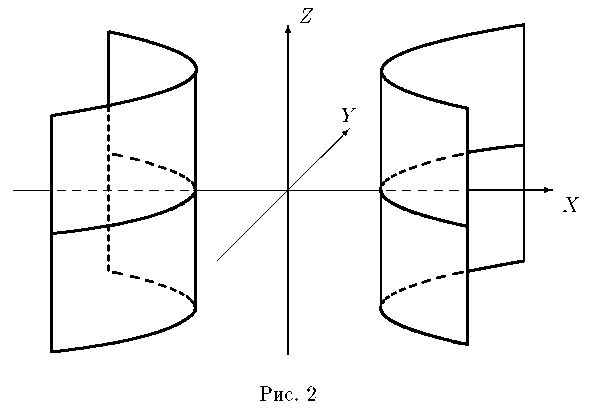
Параболический цилиндр. Уравнение
| y2 = 2px ( p>0 ) |
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является парабола (рис. 3).